こんにちは。前回は「顔の特徴点の検出」について書かせて頂きました。もしご興味のある方は前回の記事もご覧になってください。今日は「メッシュ生成(ドロネーの三角形分割)」について書いていきます。
- 顔の特徴点の検出
- ドロネーの三角形分割でメッシュ生成
- 三角形をワープしてブレンド
あわせて読みたい


顔モーフィング(1.顔の特徴点の検出)
こんにちは。 毎週木曜日の19時はVS嵐を見ることが習慣になっています。その中にある「顔ミックス対決」にトライしたので、分解して少しずつ記事にしていこうと思い...
目次
ドロネーの三角形分割
ドロネーの三角形分割は以下です。
ドロネー図は, 各三角形の外接円が他の点を内部に含まない三角形分割であり, 平面で最小角最大, 一般次元でも最大最小包含円最小など最適化基準を満たす.
引用:Weblio
 mami
mami要するに、正三角形に近い形で綺麗に三角形分割していく、という事なんだそうです。
では、なぜ顔モーフィングをするのに、ドロネーの三角形分割を使用するのか、というと、トポロジー的に(図形と図形の空間的な位置関係を表現する概念)同じそれぞれ1組の三角形分割は、平面性を維持しながら相互にモーフィングできることが証明されているから、だそうです。この説明で「そうか!なるほど!」という方はいらっしゃらないと思いますが(笑)、証明されてるんなら…、って事で進めます。気になる方は調べてみてください。
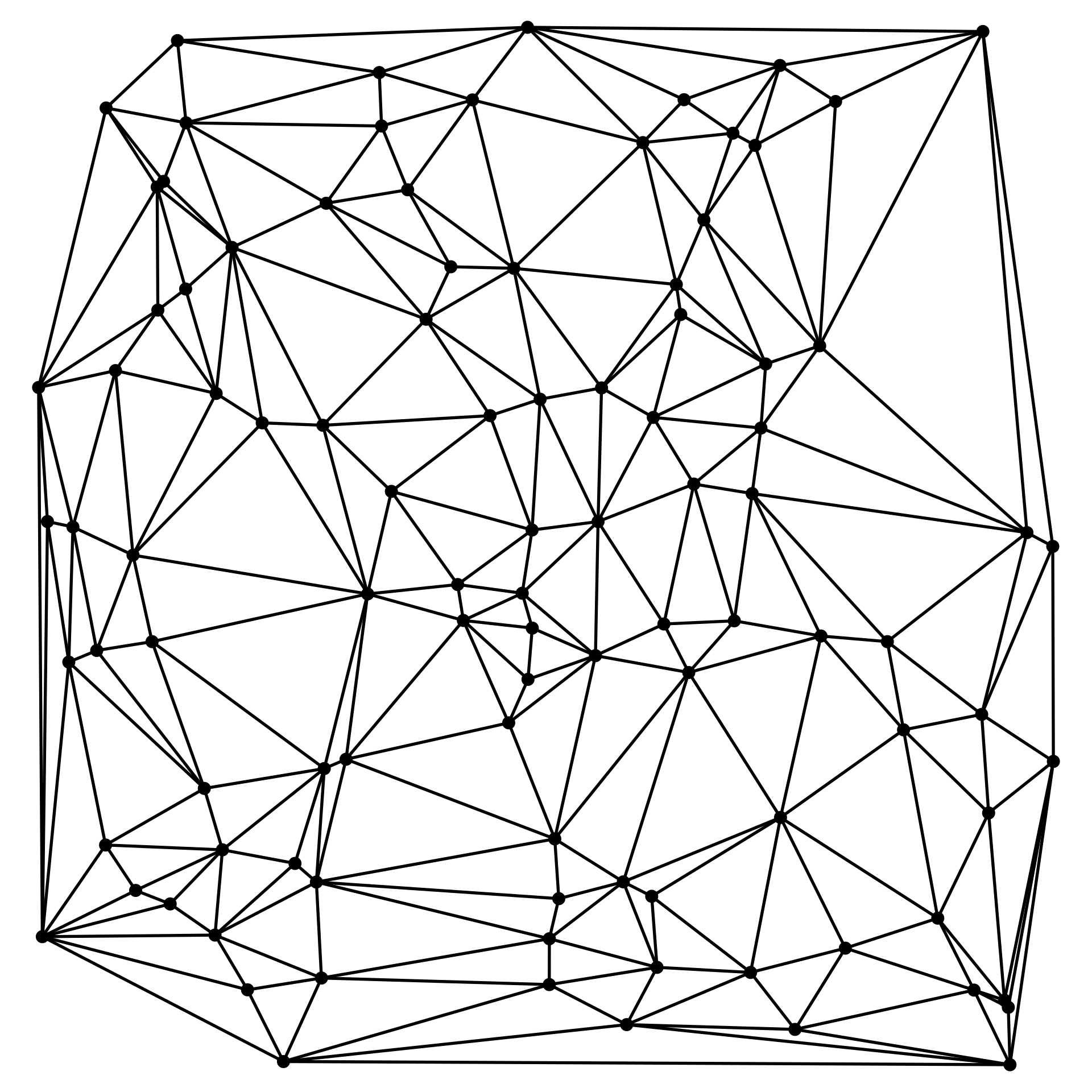
ドロネーの三角形分割した結果が分かりやすいように線を引きます。なんか怖い感じになってしまいました。
オードリーヘップバーン
[colwrap]
[col2]


[/col2]
[col2]


[/col2]
[/colwrap]
マリリンモンロー
[colwrap]
[col2]


[/col2]
[col2]


[/col2]
[/colwrap]
ソースコード
spmallick/learnopencvのソースを参考に使い回ししやすいようにさせてもらいました。素晴らしいソース群なので是非ご覧になってみてください。
import argparse
import cv2
import numpy as np
import random
def Face_delaunay(rect,points1 ,points2 ,alpha ):
points = []
for i in range(0, len(points1)):
x = ( 1 - alpha ) * points1[i][0] + alpha * points2[i][0]
y = ( 1 - alpha ) * points1[i][1] + alpha * points2[i][1]
points.append((x,y))
triangles, delaunay = calculateDelaunayTriangles(rect, points)
cv2.destroyAllWindows()
return triangles, delaunay
def calculateDelaunayTriangles(rect, points):
subdiv = cv2.Subdiv2D(rect)
for p in points:
subdiv.insert(p)
triangleList = subdiv.getTriangleList()
delaunayTri = []
pt = []
for t in triangleList:
pt.append((t[0], t[1]))
pt.append((t[2], t[3]))
pt.append((t[4], t[5]))
pt1 = (t[0], t[1])
pt2 = (t[2], t[3])
pt3 = (t[4], t[5])
if rectContains(rect, pt1) and rectContains(rect, pt2) and rectContains(rect, pt3):
ind = []
for j in range(0, 3):
for k in range(0, len(points)):
if(abs(pt[j][0] - points[k][0]) < 1.0 and abs(pt[j][1] - points[k][1]) < 1.0):
ind.append(k)
if len(ind) == 3:
delaunayTri.append((ind[0], ind[1], ind[2]))
pt = []
return triangleList,delaunayTri
def rectContains(rect, point) :
if point[0] < rect[0] :
return False
elif point[1] < rect[1] :
return False
elif point[0] > rect[0] + rect[2] :
return False
elif point[1] > rect[1] + rect[3] :
return False
return True
ご興味のある方は「3.三角形をワープしてブレンド」も是非ご覧ください。
あわせて読みたい




顔モーフィング(3.三角形をワープしてブレンド)
こんにちは。顔モーフィングの記事3本目で今回が最後です。今日は「三角形をワープしてブレンド」について書いていきます。もしご興味のある方は前回の記事もご覧にな...





コメント